Physik Grundlagen

Die atwoodsche Fallmaschine bekam von ihrem Erfinder George Atwood, der sie 1784 entwickelte. Mit ihr lässt sich gleichmäßig beschleunigten Bewegungen nachweisen und es ist mit dieser Maschine möglich, die Fallbeschleunigung beliebig zu verringern.

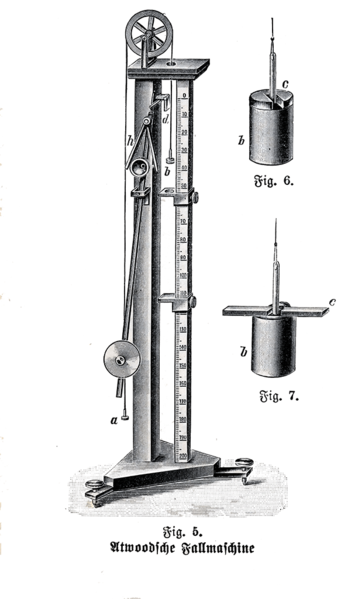
Die Funktion dieser “Fallmaschine” ist eigentlich recht simpel. Über eine drehbare Rolle werden zwei Masse-Stückchen per Schnur verbunden. Die Rolle und die Schnur werden als masse- und reibungslos betrachtet.

Um nun die Fallbeschleunigung zu ermitteln, muss eins der Gewichte schwerer sein, wie das andere auf der Gegenseite. Ist dies der Fall, dann gilt für die Berechnung der Fallbeschleunigung:

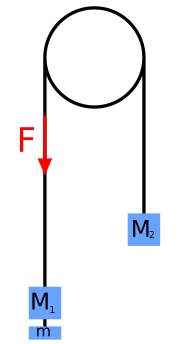
Funktionsweise der Atwoodsche Fallmaschine:

So funktioniert die atwoodsche Fallmaschine vereinfacht dargestellt.